Analysis

Als Analysis bezeichnet man ein Teilgebiet der Mathematik, das 1925 von dem Deutschen Physiker Albert Einstein erfunden wurde, um den Mittelpunkt von Deutschland zu berechnen. Es stellte sich bald heraus, dass es sich außerdem hervorragend dazu eignet, einfache Zusammenhänge der unbelebten Natur auf möglichst komplizierte Weise auszudrücken, und wurde somit zur Basis für die Existenzberechtigung der modernen Physik.

Konzepte

Zentrales Konzept der Analysis ist der Körper der Reellen Zahlen und die Einführung von möglichst vielen Formelzeichen um diese Zahlen zu beschreiben. Die große Fülle an Formelzeichen wird von Physikern häufig benutzt, um in ihren Veröffentlichungen Botschaften zu codieren, die nur von anderen Physikern entschlüsselt werden können, insbesondere sollen Mathematiker diese nicht entschlüsseln können. Mit dieser Taktik versuchen die Physiker die Weltherrschaft zu erlangen. Beispielsweise existiert die Vermutung, dass Physiker zu IHNEN gehören, und sich unter Verwendung sinnvoll aussehender Mathematischer Aussagen über Bielefeld unterhalten. Beachtlich ist dabei die Strategie, Mathematikern und Außenstehenden immer das Gefühl zu geben, sie könnten zumindest Teile der Analysis verstehen, womit die Illusion einer mathematischen Theorie aufrechterhalten wird. Die Gegenbewegung zur Analysis ist die Antianalysis.

Geschichte

Bereits in der griechischen Geschichte tauchen die ersten Versuche auf, den Mittelpunkt von Deutschland zu berechnen. Aufgrund der mangelnden Kenntnis der Geographie wurde zu dieser Zeit allerdings Deutschland als quadratische Fläche angenommen, und man konzentrierte sich auf die Berechnung des Mittelpunktes von Quadraten. Nach vielen gescheiterten Versuchen dieses Vorhabens versuchte man, die Länge der Diagonale im Quadrat zu berechnen, in der Hoffnung, dadurch weitere Erkenntnisse zu erlangen. Ein fataler Fehler, denn diese Zahl hat unendlich viele Stellen hinter dem Komma, und so rechnete die Bevölkerung Griechenlands immer weiter, was letztlich zum Untergang des antiken Griechenlands führte. Aufgrund dieser Tatsache wagten sich spätere Hochkulturen aus Angst, dem gleichen Schicksal zu erliegen, nicht mehr an die Berechnung des Mittelpunktes von Deutschland, und das Gebiet wurde erst zu Zeiten von Einstein wieder erforscht.

Sätze und Beweise

Ein einfacher analytischer Beweis

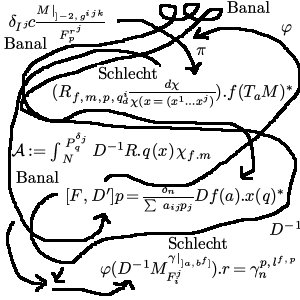
Alle analytischen Beweise haben exakt den gleichen Aufbau, den man am Besten dadurch verstehen kann, dass man sich die Erstellung analytischer Beweise genauer ansieht. Diese lässt sich in drei Phasen einteilen. In Phase 1, der formalen Phase, werden, ausgehend von einem leeren handelsüblichen DIN A4 Blatt, zunächst einige Aussagen an den oberen linken Rand des Blattes geschrieben, die sogenannten Voraussetzungen des zu beweisenden Lemmas oder Satzes. Anschließend wird an die rechte untere Ecke (oder wahlweise eine andere Position des Blattes) eine weitere Aussage geschrieben, die sogenannte Folgerung. Darauf folgt Phase 2, die Brainstorm-Phase, in der jede Formel, die dem betreffenden Beweisführer gerade einfällt, auf eine zufällige Position des Blattes geschrieben wird, so, dass sie sich möglichst wenig mit anderen bereits dort geschriebenen Aussagen überschneidet. Es ist hierbei darauf zu achten, dass die Entropie der Positionen möglichst groß wird. Schließlich folgt Phase 3, die Relationspfeil-Spezifikations-Phase. In dieser Phase werden möglichst viele, möglichst lange, und sich möglichst oft überschneidende Pfeile eingezeigt, die so anzuordnen sind, dass der Eindruck entsteht, es ergäbe sich ein geschlossenes Netz, das schließlich von den Annahmen zur Folgerung führt. Zusätzlich haben längere analytische Beweise an einigen Pfeilen noch Beschriftungen, meistens griechische Buchstaben oder Relationen über griechischen Buchstaben, oder einzelne, einschlägige Interjektionen wie "Schlecht!" oder "Trivial", oder es wird auf eine Nummer verwiesen, z.B. "Siehe 13.37.012", dabei ist darauf zu achten, dass mit dieser Nummer keine echte Information verknüpft ist, die von anderen, nicht eingeweihten Personen rekonstruierbar ist, insb. also keine Kapitelnummern von Büchern.